Тема диссертации: Методика идентификации параметров математической модели ЛА на основе синтеза следящей системы
или
Заказать новую работу(фрагменты работы)
| Учебное заведение: | Вузы города Нижний Новгород > Нижегородский государственный технический университет им. Р.Е. Алексеева |
| Тип работы: | Диссертации |
| Категория: | Высшая математика |
| Год сдачи: | 2021 |
| Количество страниц: | 89 |
| Оценка: | 5 |
| Дата публикации: | 08.08.2021 |
| Количество просмотров: | 320 |
| Рейтинг работы: |
Актуальность данной методики состоит в уточнении параметров математической
модели летательного аппарата, а конкретно аэродинамических коэффициентов полученных
при продувках летательного аппарата, что в свою очередь играет немаловажную роль при
разработке системы стабилизации и управления, а также при математическом
моделировании по результатам проведенных опытных работ.
Цель
Идентифицировать параметры математической модели летательного аппарата.
Задача
Для достижения поставленной цели необходимо решить следующие задачи:
получить и рассчитать параметры из опытной работы;
разработать следящую систему;
промоделировать работу следящей системы;
использовать метод наименьших квадратов/
СОДЕРЖАНИЕ
НОРМАТИВНЫЕ ССЫЛКИ ……………………………………...………………………...... 7
ОПРЕДЕЛЕНИЯ, ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ……………………..……………... 8
ВВЕДЕНИЕ………………………………………………………………...………………....... 9
1 Описание математической модели ОУ……………………………………………………... 10
1.1 Модуль расчета аэродинамических характеристик ОУ………………………………. 10
1.2 Модуль расчета массоинерционных характеристик....................................................... 12
1.3 Модуль двигательных установок……………………………………………….............. 12
1.4 Модуль расчета параметров стандартной атмосферы.................................................... 12
1.5 Модуль рулевых приводов…………………………………………………...…............. 12
1.6 Модуль динамических уравнений пространственного движения центра масс…....... 13
2 Основная идея методики………………………………………………………….…...…...... 15
3 Идентификация параметров продольного движения……………………………….……... 16
3.1 Идентификация коэффициентов подъемной силы…………………………………….. 16
3.2 Идентификация коэффициентов продольного момента………………………………. 32
4 Организационно-экономическая часть……………………………………………….…….. 42
4.1 Организация конструкторско-технологической подготовки производства…............ 42
4.1.1 Исходные данные по НИР……………………………………………………….... 42
4.2 Расчет себестоимости темы НИР……………………………………………………… 43
4.3 Затраты на подготовку технологической документации по существующей
технологии……………………………………………………………………………………… 49
4.4 Затраты на подготовку технологической документации при использовании
разработок НИР………………………………………………………………………………... 51
4.5 Определение годового экономического эффекта и срока окупаемости…………..... 54
5 Безопасность и экологичность проектных решений………………………………..……... 56
5.1 Обеспечение электробезопасности при эксплуатации ЭВМ……………………….... 56
5.2 Негативные факторы производственной среды……………………………….……… 60
ЗАКЛЮЧЕНИЕ……………………………………………………………….………………... 66
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ………………………………………..... 67
ПРИЛОЖЕНИЕ А. Слайды презентации…………………………………..…………............ 68
ПРИЛОЖЕНИЕ Б. Листинги программ….………..…………………………………………. 82
(фрагменты работы)
Промоделируем полет летательного аппарата на ЦКМ с условиями опытной работы.
Первое моделирование полета ЛА было выполнено с коэффициентом продольного
момента до идентификации, а второе после.
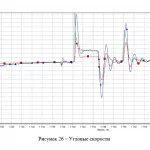
На рисунках 25, 26 представленны графики угловых скоростей из опытной работы
летательного аппарата, модели и полученной после уточнения коэффициента продольного
момента.
Согласно рисунку 25, графики угловых скоростей достаточно похожи , но тем не
менее , в соответсвии с рисунком 26 наблюдается различие.
В соответствии с рисунком 26 график угловой скорости из опытной работы, который,
очевидно, представлен в виде зашумленной линии больше напоминает график
получившейся угловой скорости после уточнения коэффициента продольного момента