Тема курсовой работы: ДИАМЕТРЫ ЛИНИИ ВТОРОГО ПОРЯДКА
или
Заказать новую работу(фрагменты работы)
| Учебное заведение: | Другие города > ДРУГОЕ |
| Тип работы: | Курсовые работы |
| Категория: | Геометрия |
| Год сдачи: | 2018 |
| Количество страниц: | 25 |
| Оценка: | отлично |
| Дата публикации: | 13.11.2021 |
| Количество просмотров: | 311 |
| Рейтинг работы: |
Геометрия
на плоскости изучает линии второго порядка. Осваивая этот материал мы должны
знать об общем уравнении линии второго порядка, асимптотических
направлениях, центре линии второго порядка, сопряженных направлениях, ее
главных направлениях и главных диаметрах.
Цель
курсовой работы: освоить понятие и свойства диаметров линии второго порядка
и применить их при решении задач.
Задачи,
поставленные для достижения цели:
1.
Изучить учебную литературу по теме курсовой работы;
2.
Подобрать и решить геометрические задачи на нахождение диаметров линии второго
порядка.
Работа
состоит из введения, двух параграфов, заключения и списка литературы.
В
первом параграфе рассматривается основная теория по теме.
Во
втором параграфе приведены подробные решения задач.
(фрагменты работы)
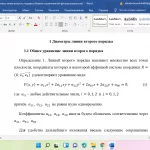
1.4 Диаметры линии второго порядка. Сопряженные направления
Теорема 2. Множество середин всех хорд линии (1), параллельных вектору p ⃗(p_1,p_2) неасимптотического направления, есть прямая, заданная уравнением
(a_11 p_1+a_12 p_2 )x+(a_21 p_1+a_22 p_2 )y+a_10 p_1+a_20 p_2=0 (9)
Определение 4. Эта прямая d называется диаметром, сопряженным хордам, направление которых определяется вектором p ⃗. Также, диаметр сопряжен вектору p ⃗.
Свойства диаметров линии второго порядка:
Если линия второго порядка γ имеет центр, то он принадлежит диаметру.
Любой диаметр нецентральной линии второго порядка имеет асимптотическое направление ⇒ направление диаметра не зависит от направления тех хорд, которые он делит пополам, т.е. любые два диаметра нецентральной линии параллельны.
Любая прямая неасимптотического направления, проходящая через центр центральной линии второго порядка, является её диаметром.
Теорема 3. Если диаметр d_1 центральной линии второго порядка является множеством середин хорд, параллельных диаметру d_2, то диаметр d_2 является множеством середин хорд, параллельных диаметру d_1.
Определение 4. Два диаметра центральной линии второго порядка называются сопряженными, если каждый из них делит пополам хорды, параллельные другому диаметру.
Определение 5. Направление ненулевого вектора p ⃗(p_1,p_2) называется сопряженным с направлением ненулевого вектора q ⃗(q_1,q_2) относительно линии, заданной уравнением (1), если выполняется равенство
a_11 p_1 q_1+a_12 p_1 q_2+a_21 p_2 q_1+a_22 p_2 q_2=0 (10)
Сопряженные диаметры центральной линии второго порядка имеют сопряженные направления.
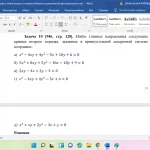
Задача 7 [940, стр. 120]. Составить уравнения двух сопряженных диаметров кривой x^2-6xy+2y^2-6x-7=0, один из которых параллелен прямой x-4y+5=0.
Решение
γ: x^2-6xy+2y^2-6x-7=0
α: x-4y+5=0
a_11=1,a_12=-3,a_22=2,a_10=-3,a_20=0,a_00=-7
Найдем направляющий вектор α
p ⃗ {-B,A} ⟹ p ⃗ {4,1}
d: (a_11 p_1+a_12 p_2 )x+(a_21 p_1+a_22 p_2 )y+a_10 p_1+a_20 p_2=0
Подставим коэффициенты кривой γ
d: (p_1-3p_2 )x+(2p_2-3p_1 )y-3p_1=0
d_1: (4-3)x+(2*1-3*4)y-3*4=0
x-10y-12=0
p ⃗ {4,1} должен быть сопряжен с q ⃗ {q_1,q_2}, относительно которого мы найдем d_2
a_11 p_1 q_1+a_12 p_1 q_2+a_21 p_2 q_1+a_22 p_2 q_2=0
1*4*q_1-3*4*q_2-3*1*q_1+2*1*q_2=0
4q_1-12q_2-3q_1+2q_2=0
q_1=10q_2
Возьмем q_1=10,q_2=1 ⟹ q ⃗ {10,1}
Задача 10 [946, стр. 120]. Найти главные направления следующих кривых второго порядка, заданных в прямоугольной декартовой системе координат:
а) x^2-4xy+4y^2-5x+10y+6=0
б) 〖5x〗^2+8xy+5y^2-18x-18y+9=0
в) 2xy-4x+2y-3=0
г) x^2-4xy+4y^2-5x+6=0
д) x^2+xy+2y^2-3x+y=0
Решение
(a_22-a_11 ) p_1 p_2+a_12 (p_1^2-p_2^2 )=0
а) 〖γ: x〗^2-4xy+4y^2-5x+10y+6=0
a_11=1, a_22=4,〖 a〗_12=-2
a_12≠0 ⟹ p ⃗≠0 (т. к. p ⃗≠0)
Положим k=p_2/p_1 ⟹ k^2 a_12+(a_11-a_22 )k-a_12=0
k_1,2=(a_22-a_11±√((a_11-a_22 )^2+4a_12^2 ))/(2a_12 )
Подставим коэффициенты кривой γ
k_1=(4-1+√((4-1)^2+4*〖(-2)〗^2 ))/(2*(-2))=(3+5)/(-4)=-2
k_1=p_2/p_1 ⟹ -2=p_2/p_1 ⟹ p_2=-2p_1
Возьмем p_1=1,p_2=-2 ⟹ p ⃗ {1,-2}
k_2=(4-1-√((4-1)^2+4*〖(-2)〗^2 ))/(2*(-2))=(3-5)/(-4)=1/2
k_2=p_2/p_1 ⟹ 1/2=p_2/p_1 ⟹ p_1=2p_2
Возьмем p_1=2,p_2=1 ⟹ p ⃗ {2,1}
б) γ: 〖5x〗^2+8xy+5y^2-18x-18y+9=0
a_11=5, a_22=5,〖 a〗_12=-4
a_12≠0 ⟹ p ⃗≠0 (т. к. p ⃗≠0)
Положим k=p_2/p_1 ⟹ k^2 a_12+(a_11-a_22 )k-a_12=0
k_1,2=(a_22-a_11±√((a_11-a_22 )^2+4a_12^2 ))/(2a_12 )
Подставим коэффициенты кривой γ
k_1=(5-5+√((5-5)^2+4*4^2 ))/(2*4)=(0+8)/8=1