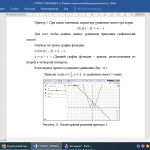
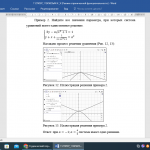
Тема дипломной работы: Методика изучения систем уравнений при обучении математике в основной школе
или
Заказать новую работу(фрагменты работы)
| Учебное заведение: | Учебные заведения Москвы > Московский городской педагогический университет (МГПУ) > Математический факультет |
| Тип работы: | Дипломные работы |
| Категория: | Педагогика |
| Год сдачи: | 2021 |
| Количество страниц: | 58 |
| Оценка: | 5 |
| Дата публикации: | 22.09.2023 |
| Количество просмотров: | 62 |
| Рейтинг работы: |
Актуальность темы: современное
общество - это индустриальное или постиндустриальное (информационное) общество,
в котором наука, знания, технологии и образование играют важную роль. В
современном мире математика сопровождает человека на протяжении всей его жизни.
Люди всех профессий так или иначе применяют математические знания. Кроме того,
математические знания используются в повседневной жизни, и это не только
простые математические вычисления, но и теория вероятностей, элементы высшей
математики. Это потому, что математика предлагает достаточно четкие модели для
изучения окружающей действительности.
Важнейшей причиной
потребности человечества в математике является воспитание в человеке
самостоятельности, способности брать на себя ответственность, способности
проявлять инициативу, быть готовым замечать проблемы, уметь мыслить, логически
размышлять, анализировать, сравнивать.
Известно, что на
протяжении многих лет алгебру рассматривали как науку об уравнениях и способах
их решения. Большое значение уравнений подчеркивал А. Эйнштейн. Он говорил:
"Мне приходилось делить свое время между политикой и уравнением. Однако
уравнение, на мой взгляд гораздо важнее, потому что политика существует только
для данного времени, а уравнения будут существовать вечно".
При подготовке к
математической олимпиаде, государственному экзамену, ученики сталкиваются с
большим количеством уравнений, которые необходимо выполнить за ограниченное
время. Среди них часто встречаются такие, что проверяют у обучающихся не
столько технические навыки, сколько внимание, умение найти кратчайший путь
решения, применить нестандартный, оригинальный метод и т. д., данные уравнения
не содержали тяжелых расчетов, но с их помощью обучающиеся могли
продемонстрировать наглядное, эффективное, а иногда и неожиданное применение теоретического
материала.
Объект исследования – процесс
обучения математике в основной школе.
Предмет исследования –
методика решения систем уравнений в процессе обучения математике.
Цель исследования –
обобщение и систематизация методов решения систем уравнений, разработка
методики обучения решению систем уравнений на уроках математики.
Задачи:
1.
Рассмотреть понятие уравнений и систем уравнений,
методы решения систем уравнений;
2.
Изучить возрастные особенности обучающихся
3.
Разработать методические рекомендации по обучению
решению систем уравнений в курсе алгебры основной школы.
Содержание
Введение. 2
Глава 1.
Теоретические аспекты обучения по теме «Уравнения. Системы уравнений» 4
1.1. Понятие
уравнений и систем уравнений. 4
1.2. Методы
решения систем уравнений. 7
1.3. Возрастные
особенности обучающихся. 10
1.4. Логико-математический
анализ темы «Уравнение с двумя переменными и их системы». 13
Глава 2. Методические аспекты изучения систем уравнений в
основной школе. 19
1.1. Методика
формирования предметной математической компетентности при изучении темы
«Уравнения с двумя переменными и их системы». 19
2.2. Методы, формы и средства в формировании предметной
компетентности при изучении темы «Уравнение с двумя переменными и их системы». 32
Заключение. 52
Список литературы: 53
Приложение 1. 59
Приложение 2. 64
(фрагменты работы)
1.3. Возрастные особенности обучающихся
Согласно исследованиям психологов (Божович Л., Эльконин Д., Кон И., Реан А.) было установлено, что младший подростковый возраст определяется значительными новообразованиями: потребность в общении, формирование самосознания, самооценки, возникновение чувства взрослости как особой формы самосознания, способность к рефлексии, расширение социально-коммуникативных контактов [2].
Интересы учеников играют важную роль в процессе восприятия и усвоения учебного материала. Интересы, мотивация, потребности подростков динамичны, очень нестабильны.
Задачи должны, как применять полученные знания в повседневной жизни и различных отраслях науки и производства (расчеты домашнего бюджета; коммерческие вычислительные операции; чтение графических изображений (строительство дачных сооружений, несложные ремонтные работы, понимание инструкций, схем принципа действия бытовых приборов и механических средств); моделирование одежды, разнообразная дизайнерская работа и др.), применение математических знаний в экологии, геодезии, кулинарии, музыке, строительстве, архитектуре и т.д.).
Материал не содержащий упражнений и задач, направленных на развитие творчества, инициативы, самостоятельности теряет для учащегося актуальность и привлекательность.
У учащихся 5 – 6 классов начинает формироваться способность понимать других людей, сосуществовать с ними на принципах равноправия и толерантности. Это требует диалогового обучения, создания в системе задач ситуаций, решая которые подростки учатся учитывать разные взгляды, отстаивать собственные, предусматривать результаты их, обосновывать целесообразность и т.д.
Логическое мышление, характерное для этого возраста, создает предпосылки для формирования доказательной речи, исследовательских черт и характеристик. Учащиеся учатся придерживаться логики построения рассказа, высказывать соображения и суждения, обосновывать их. Задания, решение которых связано с доказательством правильности (ложности) суждений, обоснованием, опровержением представленной информации, исправлением ошибок и т.п., совершенствуют характеристики монологической речи учащихся: логику, содержательность, образность. Для улучшения осмысленного понимания новых терминов и понятий важно удачно проиллюстрировать их примерами, связанными с приобретенным учащимися личностным жизненным опытом, предлагать творческие задачи. Второстепенную информацию, которая может только запутать ученика, целесообразно сводить к минимуму. Задачи должны содержать разные типы примеров – вербальные, числовые, графические, символьные [5, с. 56].
Интенсивно у младших подростков развивается память, на фоне развития речи. Поэтому полезны задачи, предусматривающие словесное описание, размышление, объяснение ученика своими словами определенного понятия или явления, его графическое воспроизведение, доказывание, обоснование или опровержение приведенных положений и т.д.
В этот период усиливается стремление учащихся достигать понимания того, что запоминать и воспроизводить важно научиться своими словами, делая одновременно необходимые обобщения. В системе задач важно учитывать индивидуальные различия в умственной деятельности учащихся, которые проявляются в том, что одни из них более продуктивно работают с графическим или схематическим материалом, другие – со словесным, а третьи – одинаково успешно работают и с наглядно-образным, и словесно- логическим материалом. Поэтому важно, чтобы материал по математике был представлен разными способами кодирования информации, содержал задачи на развитие индивидуальных свойств восприятия и мышления. Новый материал будет понятен, если в процессе его изучения будут применяться все способы изложения информации (способы кодирования), будет рационально сочетаться словесный язык с графическим и символьным.
Важное значение приобретает развитие мышления (умение связывать между собой разные знания, чтобы в результате проанализировать и пересказать содержание текста; составить задачу, обратную данной; изменить условие задачи, оставив вопрос; на установление закономерностей (продолжить ряд чисел, заполнить) квадраты и др.), определение причинности описанных событий, выражение своих соображений по прочитанному, составление задач по общим характеристикам данных, по выражению, по заданному вопросу, рисунку, схеме, подбор слов, близких (противоположных) по значению, отгадывание загадок, ребусов, кроссвордов) [14].
По исследованиям психологов, на понимание учащимися задач, влияет формулировка их, причем понятнее те, у которых автор обращается непосредственно к каждому из учеников (вычисли, прочти, запиши и т.п.). Поэтому ученые советуют в формулировке задач активнее использовать глаголы – для формирования репетитивных навыков следует использовать следующие из них: определи, приведи, опиши, прочти; для формирования познавательных умений глаголы: распознай, найди, вычисли, нарисуй, оцени; в задачах на интеграцию знаний: сравни, упорядочи, построй, обобщи, сформулируй; для формирования практических навыков: осуществи, построй, выполни, начерти [25, с. 48].
Поэтому в процессе обучения учащихся 5 – 6 классов необходимо учитывать возрастные особенности раннего подросткового возраста (новообразование, особенности развития речи, общения, процессов памяти, мышления, восприятия и т.п.), познавательные интересы и возможности современных учащихся, качество языка школьных учебников, их оформление и полиграфическое исполнение.
Похожие работы
-
81 страниц |2500 ₽
-
2500 ₽
-
69 страниц |1000 ₽
-
49 страниц |2500 ₽
-
68 страниц |2200 ₽
-
900 ₽
-
151 страниц |1600 ₽
-
64 страниц |2500 ₽